
Welcome to the
KEA Research Group on
Image & Data Processing, Analysis
and
Computational Geometry
KEA is a flexible toolbox of robust methods for image, data-processing and for computational geometry tasks. It has been developed by Kewei Zhang (The University of Nottingham, UK), Elaine Crooks (Swansea University, UK) and Antonio Orlando (National University of Tucumám, Argentina).
These methods are based on novel tools that depend exclusively on the geometric structure of the image and on the particular task to be performed on the image. As such, they are fundamentally different from those methods that require comparing pixel values in a predetermined mask using some ad hoc problem-designed convolution function, or that require the solution of ad hoc problem-dependent partial differential equations.
For a sample of possible, but by no means exhaustive applications, please visit the link Applications.
Given the geometric structure of the new tools, it is possible to devise new transformations suitable for the application in object. This renders such tools very flexible and versatiles for any type of application.
Another important feature is that the transformations are performed globally on the image, the object or the data set and thus are fast and efficient. These new methods are also affine-invariant and robust under perturbation. This means that one can deform an image or an object and still recover key features
The proposed methods are partly based on our UK patent GB2488294.
 Multiscale Medial Axis Map
Multiscale Medial Axis Map
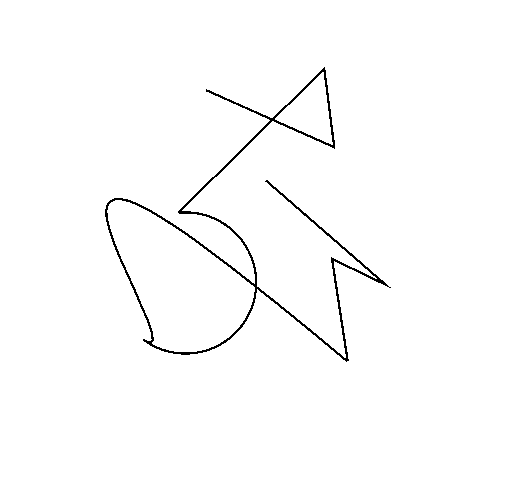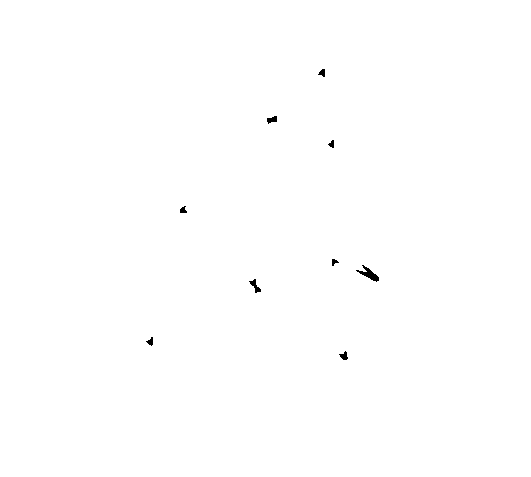 High Curvature Point Detection
High Curvature Point Detection