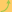-
Multiscale Medial Axis Map
- Let U be a non-empty closed subset of the Euclidean space
Rn.
The medial axis M(U) of U is the set of points x in the complement of U
that have at least two closest points
in U. If U is a bounded open set, then M(U) is the set of points in U
with at least two closest points in the boundary of U. Bounded open sets are next referred to as shape.
The medial axis provides a compact representation of the shape,
and has been used in a number of applications. It is, however, well
known that such geometric structure is unstable, for instance, with respect to the
Hausdorff distance. A small change in shape can cause a relatively large change in the corresponding medial axis. Furthermore, it must be observed that in many aplications the boundary of a shape might also not well be defined but given through sampling. In this case, therefore, the challenge is to compute an approximation of
the medial axis which catches the same topological type as of the original shape and is more stable under smmall perturbations of the shape.
The multiscale medial axis map Ml(U), with l, provides a stable continuous representation of the medial axis
with respect to Hausdorff measure and can remove
undesirable parts of the medial axis by simple thresholding. The multiscale medial axis map Ml(U)=Ml(x;U) is a scalar function with support in a neighborhood of the medial axis M(U).
The values of Ml(x;U) and its curvature depend on the strength of the boundary and on the parameter l which also controls the support width of Ml(U).
- ii) Dense uniforn sampling of the boundary
-

(a)

(b)
-
(a) Discrete set U of points from a dense uniform sampling of the boundary of an ellipse.
-
(b) Support of the multiscale medial axis map
Ml(U)=Ml(x;U) for
l=0.1 and it=1.
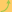
-

(a)

(b)
-
(a) Suplevel set of Ml(U) corresponding to a level value equal to 32,
l=0.1 and it =1.
-
(b) Reverse distance transform corresponding to the suplevel set of Ml(U)
displayed in (a).
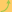
- iii) Coarse non uniforn sampling of the boundary
-

(a)

(b)
-
(a) Discrete set U of points from a coarse non uniform sampling of the boundary of an ellipse.
-
(b) Support of the multiscale medial axis map
Ml(U)=Ml(x;U) for
l=0.1 and it=1.
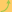
-

(a)

(b)
-
(a) Suplevel set of Ml(U) corresponding to a level value equal to 48,
l=0.1 and it =1.
-
(b) Reverse distance transform corresponding to the suplevel set of Ml(U)
displayed in (a).
- iv) Coarse non uniforn random sampling of the boundary
-
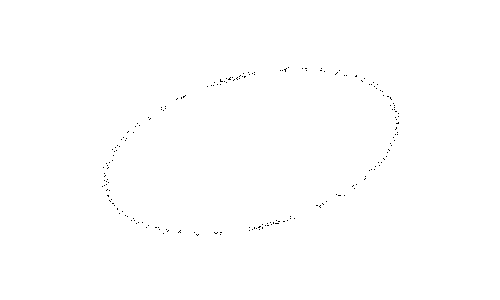
(a)
(b)
-
(a) Discrete set U of points from a coarse non uniform random sampling of the boundary of an ellipse.
-
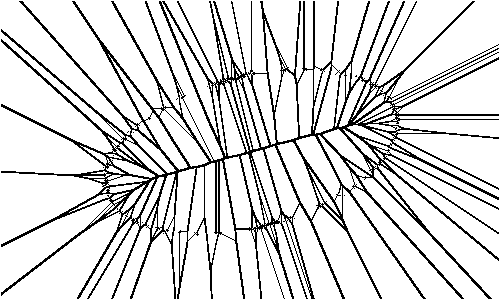
(b) Support of the multiscale medial axis map
Ml(U)=Ml(x;U) for
l=0.1 and it=1.
-

(a)

(b)
-
(a) Suplevel set of Ml(U) corresponding to a level value equal to 56,
l=0.1 and it =1.
-
(b) Reverse distance transform corresponding to the suplevel set of Ml(U)
displayed in (a).

 (a)
(a)
 (b)
(b)
 (a)
(a)
 (b)
(b)
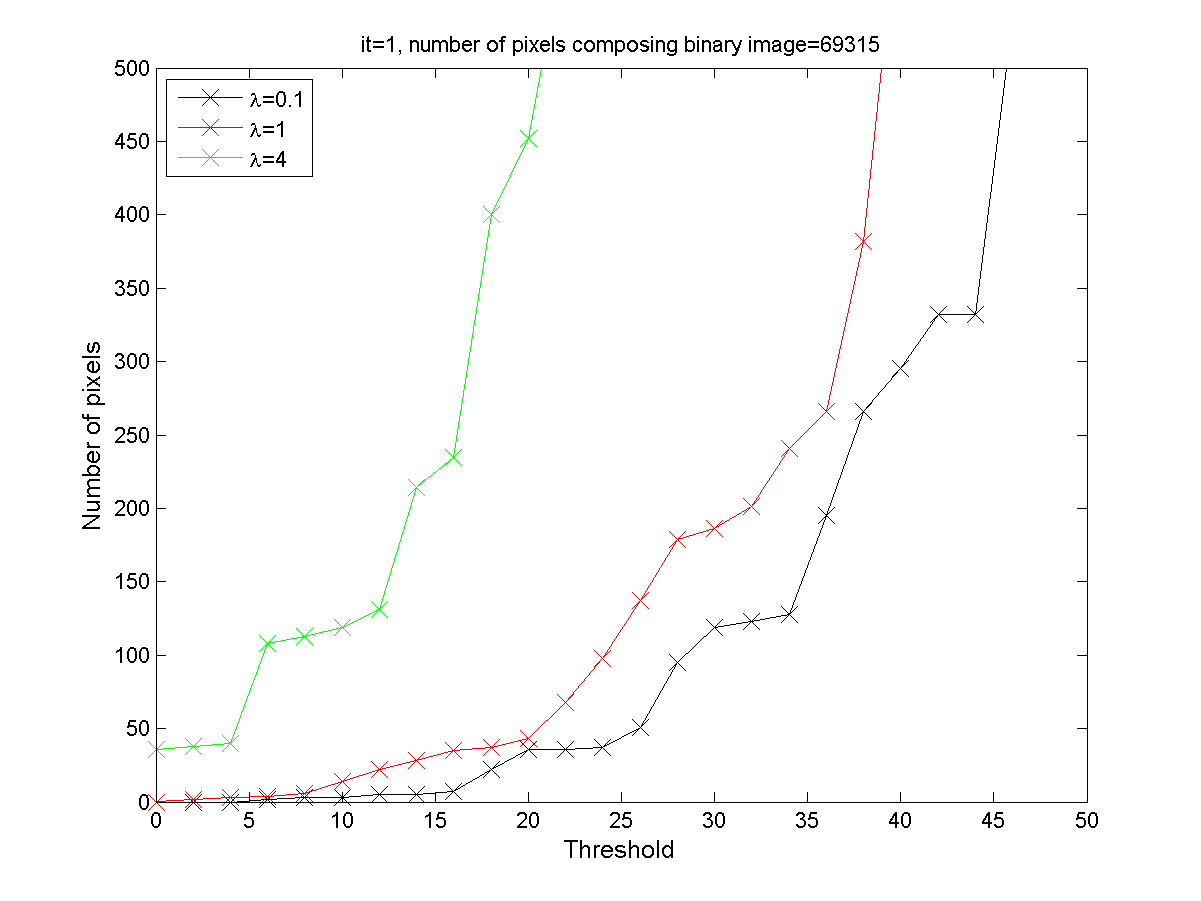 Diagram displaying for different values of the parameter l, the variation with
the threshold of the number of pixels belonging to the difference between the input image and the reconstructed one from
Ml(U) computed assuming it=1. The total number of pixels composing the binary image is 69315.
Diagram displaying for different values of the parameter l, the variation with
the threshold of the number of pixels belonging to the difference between the input image and the reconstructed one from
Ml(U) computed assuming it=1. The total number of pixels composing the binary image is 69315.
 (a)
(a)
 (b)
(b)
 (a)
(a)
 (b)
(b)
 (a)
(a)
 (b)
(b)
 (a)
(a)
 (b)
(b)
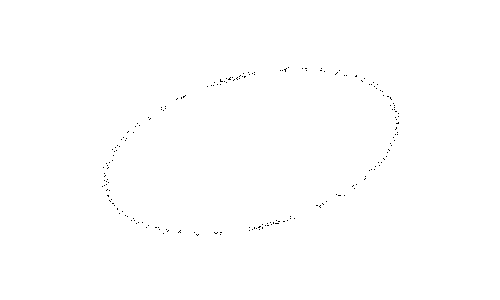 (a)
(a)
 (b)
(b)
 (a)
(a)
 (b)
(b)