Click on the pictures to see animations (in .mov format)
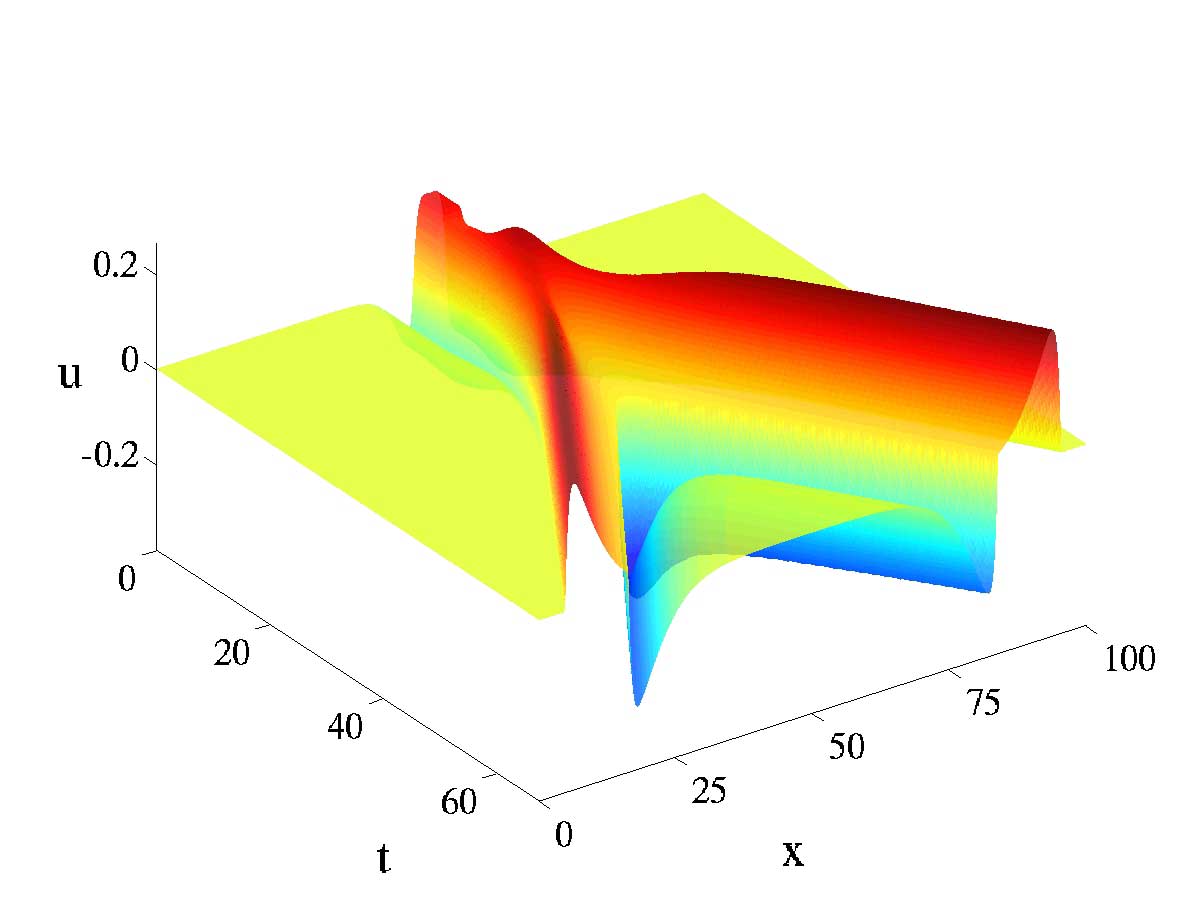
Figure 5.7. A dimple bump shedding a pair of pulses. |
Click on the pictures to see animations (in .mov format)

Figure 5.7. A dimple bump shedding a pair of pulses. |
http://www.maths.nott.ac.uk/personal/sc/evans/index.htmlstephen.coombes@nottingham.ac.uk