My research lies in the field of fluid dynamics with a focus on problems that involve moving interfaces or free surfaces. My work follows a synergistic approach that combines mathematical modelling, asymptotic analysis and numerical computations, and facilitates the study of complex fluid dynamics problems with real-life applications. I am particularly interested in identifying the physical mechanisms that induce irregular fluid phenomena, and in utilising experimental observations to verify results obtained by numerical calculations.
An up-to-date list of publications can be found here.
A detailed description of the various projects I have worked on can be found below. Click the links to go directly to each project.
- Nonlinear dynamics in multilayer shear flows
- Water wave modelling: extreme waves and impact on floating structures
- Chaos in the two-dimensional Kuramoto-Sivashinsky equation
Nonlinear dynamics in multilayer shear flows
The research aims to shed light on the role of soluble surfactants on the complex behaviour of small-scale multilayer flows, in particular on the interfacial instabilities encountered in such flows. The research approach I follow integrates different techniques such as liner stability analysis, asymptotic methods and numerical computations, with particular aim to explore the underlying nonlinear dynamics.
Asymptotic modelling of two-fluid shear flows
The nonlinear stability of two-fluid Couette/Poiseuille flows is studied using a novel evolution equation whose dynamics is validated by direct numerical simulations (Kalogirou et al., 2016; Kalogirou et al., 2020). The evolution equation incorporates inertial effects at arbitrary Reynolds numbers through a non-local term arising from the coupling between the two fluid regions, and is valid when one of the layers is thin. The equation predicts asymmetric solutions and exhibits bistability, features that are essential observations in the Couette-flow experiments of Barthelet et al. (J. Fluid Mech., vol. 303, 1995, pp. 23–53). Comparisons between model solutions and direct numerical simulations show excellent agreement.
A related study on the Rayleigh–Taylor instability at the interface of two sheared fluid can be found in Kalogirou & Blyth, 2023. This work includes: mathematical modelling that reduces the dynamics of the full problem to a lubrication equation describing the evolution of the interface, numerical solutions thereof for adverse density stratifications, and asymptotic analysis that reveals the finer structure of interfacial waves. Comparisons between the lubrication model, direct numerical simulations, and the asymptotic solutions demonstrate an excellent agreement between the three in terms of interfacial structure, wave speed and film thicknesses.
Surfactant-laden thin-film flows
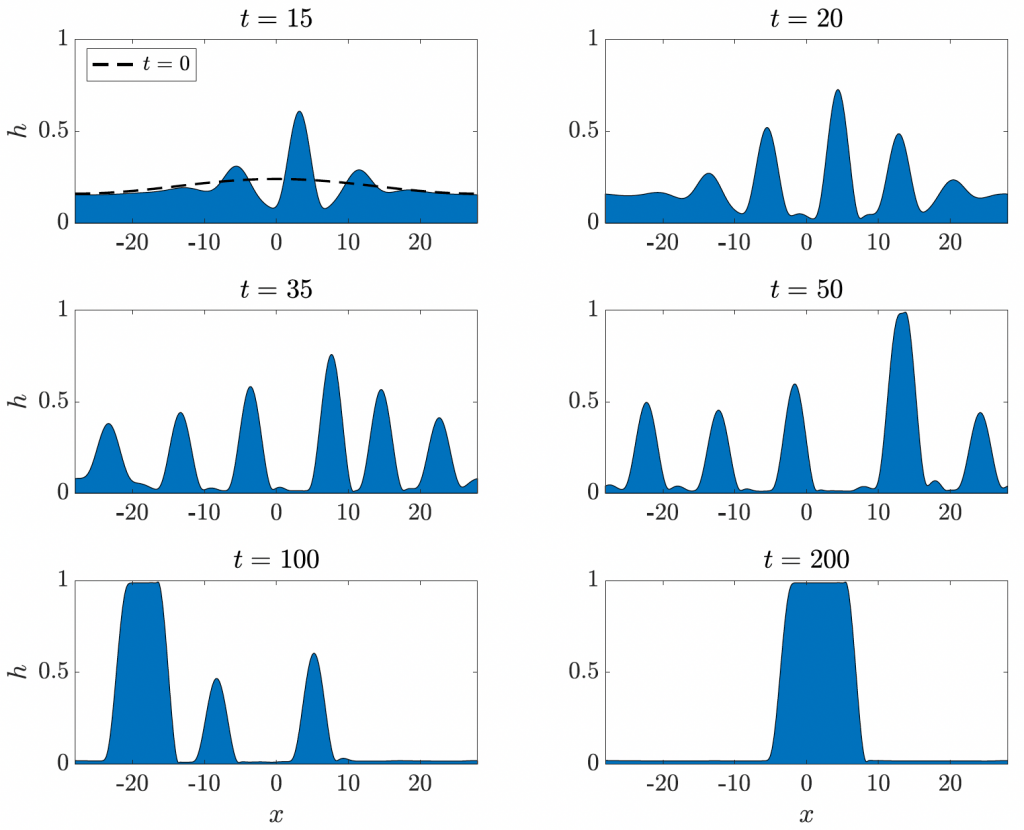
Multilayer fluid flows with a surfactant-populated interface between the fluids has been studied using mathematical modelling and asymptotic techniques (Kalogirou, 2014). Following the flows into the nonlinear regime was of particular interest in order to understand nonlinear dynamics and underlying structures. The mathematical model derived was used to classify the dynamics and stability of the solutions, through analytical (asymptotic and linear stability analysis) and numerical computations. Extensive numerical experiments reveal that the dynamics are mostly organized into travelling or time-periodic travelling wave pulses, but spatiotemporal chaos is also supported when the length of the system is sufficiently large (Kalogirou et al., 2012). It is also found that one-dimensional interfacial travelling waves of permanent form can become unstable to spanwise perturbations for a wide range of parameters, producing three-dimensional flows with interfacial profiles that travel in the direction of the underlying shear (Kalogirou and Papageorgiou, 2016). The interacting effect of surfactants, inertia, and gravity has also been investigated (Kalogirou, 2018).

The effect of soluble surfactants on interfacial stability
The stability of a two-layer surfactant-laden Couette flow is considered, using linear stability analysis (Kalogirou & Blyth, 2019) and nonlinear asymptotic modelling (Kalogirou & Blyth, 2020). One of the fluids is contaminated with a soluble surfactant whose concentration may be above the critical micelle concentration, in which case micelles are formed in the bulk of the fluid. The primary aim of this study is to determine the influence of surfactant solubility on the linear stability of the flow and the nonlinear dynamics. The lubrication approximation is applied and a strongly nonlinear system of equations is derived for the evolution of the interface and surfactant concentration at the interface, as well as the vertically averaged monomer and micelle concentrations in the bulk (as a result of fast vertical diffusion). If the surfactant exists at large concentrations that exceed the critical micelle concentration, then long interfacial waves are stable at large times, unless density stratification effects overcome the stabilising influence of micelles.
A related study of the impact of surfactant solubility on the linear stability of a semi-infinite fluid undergoing a shearing motion can be found in Kalogirou & Blyth, 2021.

Water wave modelling: extreme waves and impact on floating structures
The research concerns theoretical and numerical modelling of nonlinear water waves, in particular extreme waves, and their impact on moving structures such as wave-energy devices or ships. Variational methods are employed to derive equations governing the evolution of the free water surface, and then fast and accurate numerical simulations are performed.
Relevant videos from simulations and experiments can be found in my YouTube channel.
Extreme-wave modelling using asymptotic models
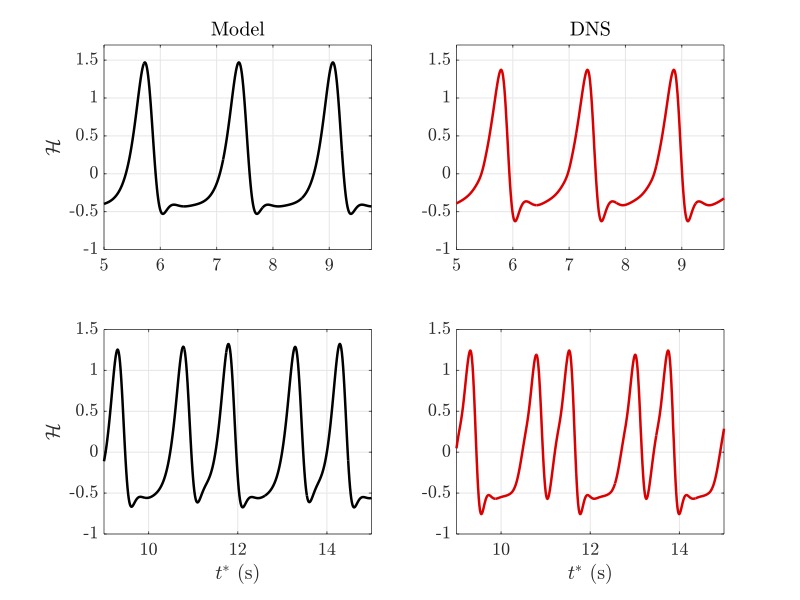
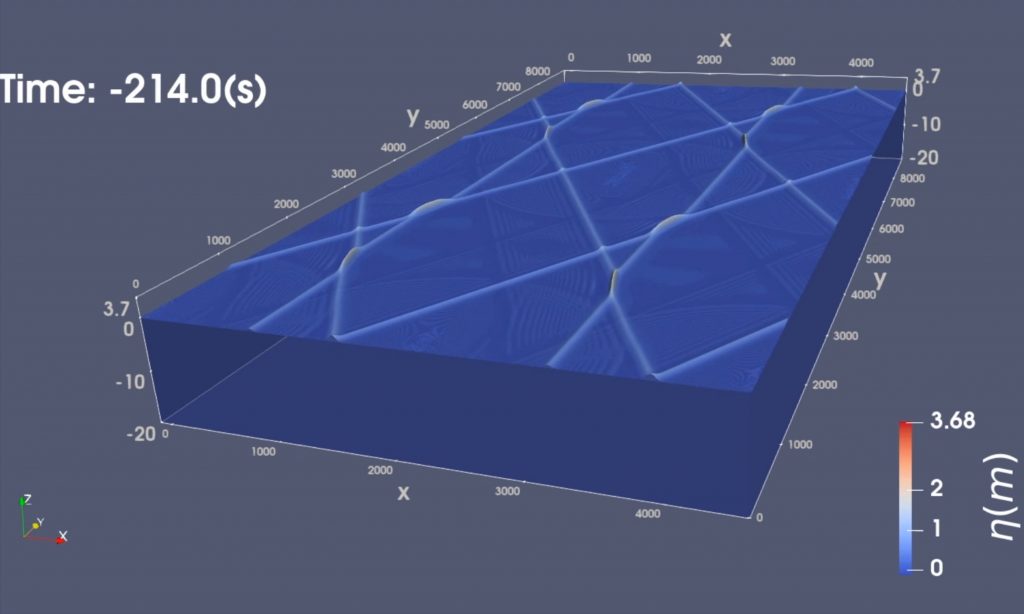
We explore extreme nonlinear water-wave amplification in a contraction or, analogously, wave amplification in crossing seas. The latter case can lead to extreme or rogue-wave formation at sea. A bore-soliton-splash of circa tenfold amplification is observed in wave-tank experiments in which a solitary-water-wave compound runs into a contraction. Mathematical modelling of such waves is then demonstrated by investigating variational methods asymptotically and numerically. A reduced potential-flow water-wave model is derived comprising the Benney-Luke equations and appropriate boundary conditions. The asymptotic model is solved numerically using a finite element method and a 2nd-order symplectic integrator for the time discretisation. The numerical results are compared to soliton-splash experiments (Bokhove and Kalogirou, 2016; Bokhove et al., 2019). The same model is also used to analyse the maximum amplification in the case of two or three obliquely-interacting solitons (Gidel et al., 2017; Choi et al., 2022).
A new wave-to-wire wave-energy model
A novel wave-energy device is developed through an experimental setup comprising wave amplification in a contraction, a wave-activated buoy, and magnetically induced energy generation (Bokhove et al., 2019a). We develop a novel wave-to-wire mathematical model of the combined wave hydrodynamics, wave-activated buoy motion and electric power generation by magnetic induction, from first principles, satisfying one grand variational principle in its conservative limit. Wave and buoy dynamics are coupled via a Lagrange multiplier, which boundary value at the waterline is in a subtle way solved explicitly by imposing incompressibility in a weak sense. Dissipative features, such as electrical wire resistance and nonlinear LED loads, are added a posteriori. New is also the intricate and compatible finite-element space-time discretisation of the linearised dynamics, guaranteeing numerical stability and the correct energy transfer between the three subsystems. Preliminary simulations of our simplified and linearised wave-energy model are encouraging and involve a first study of the resonant behaviour and parameter dependence of the device (Bokhove et al., 2019a, 2019b, 2020; Bolton et al., 2021).
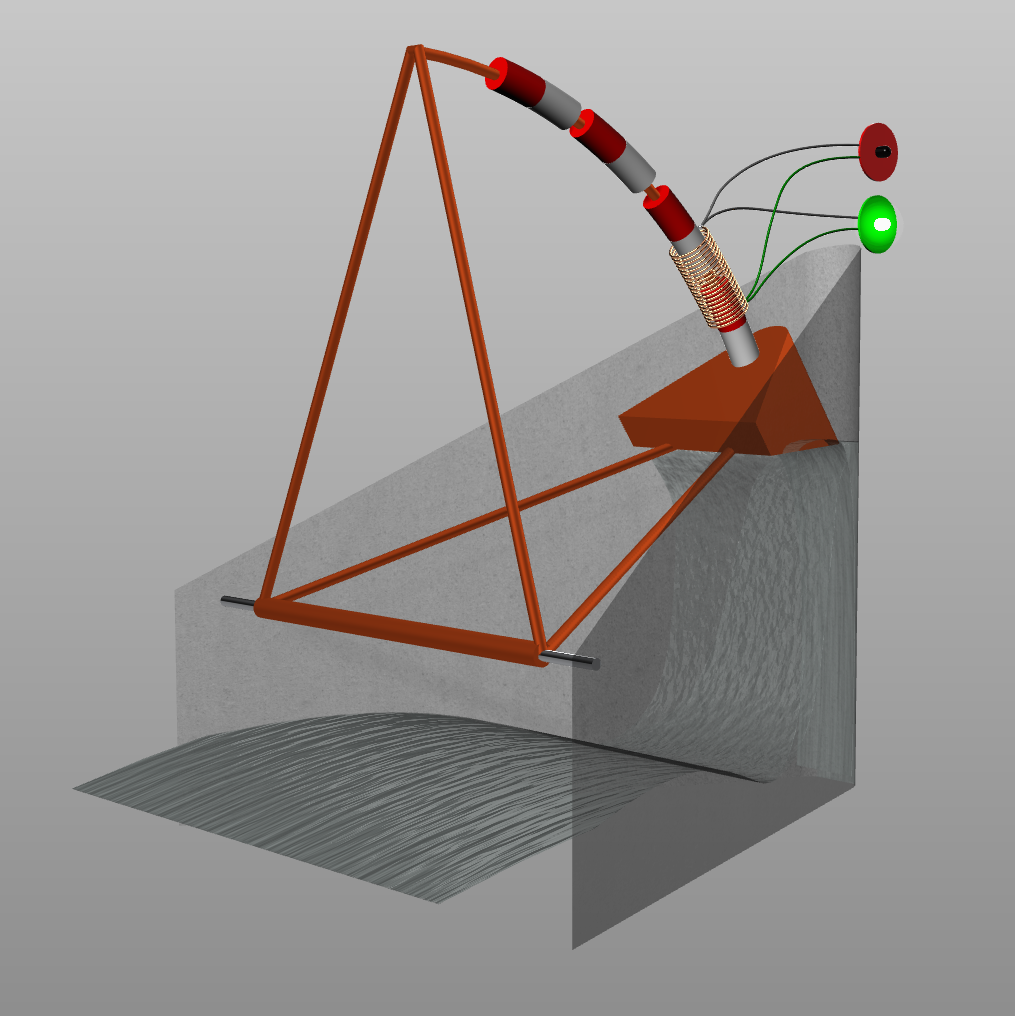
Wave impact on wave-energy buoys and moving ships
A mathematical model describing the nonlinear evolution of water waves and their interaction with moving ships or wave-energy devices is presented (Kalogirou & Bokhove, 2016; Kalogirou et al., 2017). The model is derived variationally by directly extending Luke’s variational principle to include the ship dynamics, and this results in a coupled Hamiltonian system for the wave-ship dynamics. This nonlinear system consists of the classical potential-flow water-wave equations, coupled to a set of equations describing the dynamics of the ship. The novelty of this work lies in the use of a Lagrange multiplier to impose a constraint on the water surface under the ship. We also present a model linearised around the rest steady state, which we consider a stepping stone towards solving for the nonlinear dynamics. The resulting linear variational system is discretised using (dis)continuous Galerkin finite element approximations, leading to a discrete algebraic variational principle.
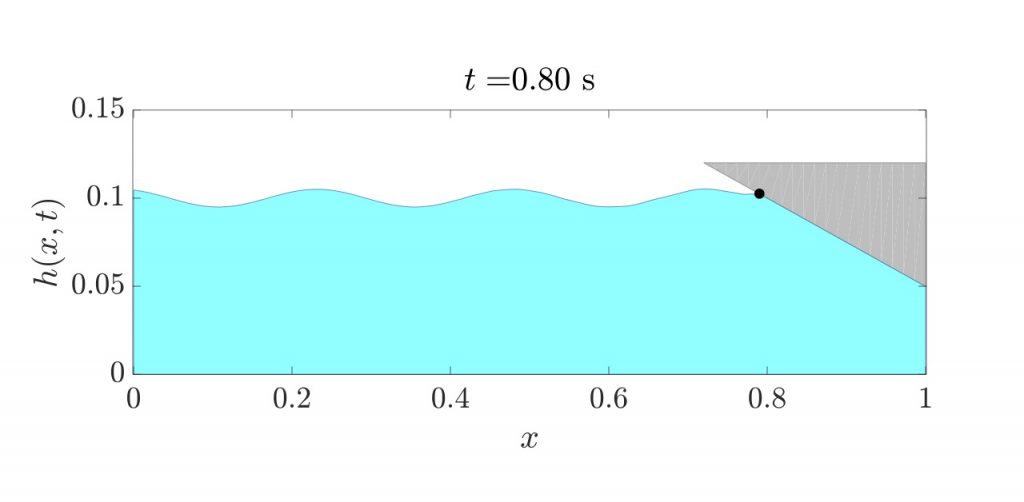
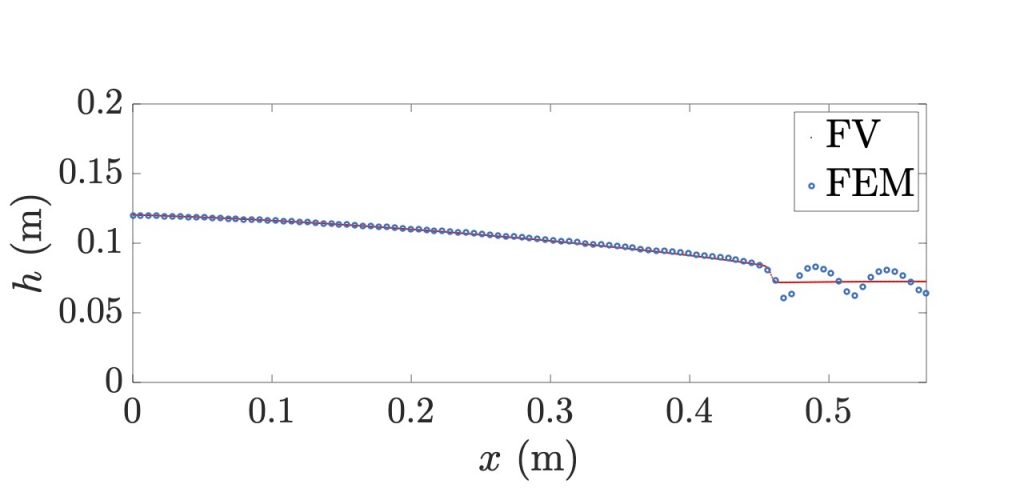
Hydrodynamics in a Hele-Shaw tank
The damped motion of driven water waves in a vertical Hele-Shaw tank is investigated variationally and numerically (Kalogirou et al., 2016). The equations governing the hydrodynamics of the problem are derived from a variational principle for shallow water. The variational principle includes the effects of surface tension, linear momentum damping due to the proximity of the tank walls and incoming volume flux through one of the boundaries representing the generation of waves by a wave pump. The model equations are solved numerically using (dis)continuous Galerkin finite element methods as well as a standard finite volume solver and are compared to exact linear wave sloshing and driven wave sloshing results. Numerical solutions of the shallow-water-wave equations are also validated against laboratory experiments of artificially driven waves in the Hele-Shaw tank.

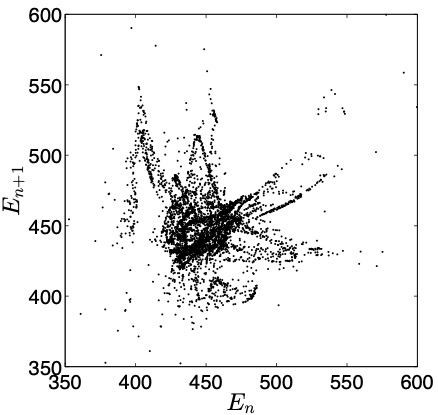
Chaos in the two-dimensional Kuramoto-Sivashinsky equation
The Kuramoto-Sivashinsky equation (KSE) in one spatial dimension is one of the most well-known and well-studied partial differential equations; it exhibits spatio-temporal chaos that emerges through various bifurcations as the domain length increases. There have been several notable analytical studies aimed at understanding how this property extends to the case of two spatial dimensions. We performed an extensive numerical study of the Kuramoto-Sivashinsky equation to complement these analytical studies (Kalogirou et al., 2015; Tomlin et al., 2018). We explored in detail the statistics of chaotic solutions and classify the solutions that arise for domain sizes where the trivial solution is unstable and the long-time dynamics are completely two-dimensional. While we find that many of the features of the 1D KSE, including how the energy scales with system size, carry over to the 2D case, we also note several differences including the various paths to chaos that are not through period doubling.
A study on the numerical analysis of linearly-implicit schemes for multi-dimensional Kuramoto–Sivashinsky–type equations can be found in Akrivis et al. (2016).