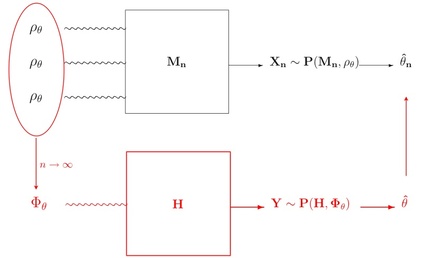
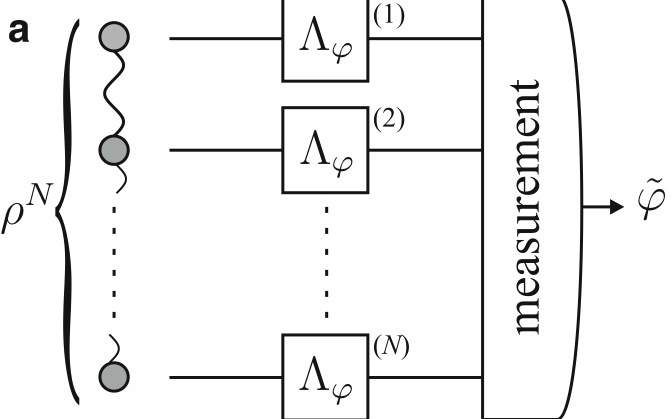
Recent research topics
Quantum Statistics
model selection, spectral thresholding in quantum tomography; quantum local asymptotic normality; quantum decision theory; quantum learning;
Quantum Metrology
achievability of the Heisenberg limit; quantum metrology and dynamical phase transitions; quantum metrology with finitely correlated states
Quantum Open Systems
system identification for linear and non-linear quantum Markov processes; large deviations and dynamical phase transitions in open systems; control of quantum open systems
Some of these topics are briefly described below:
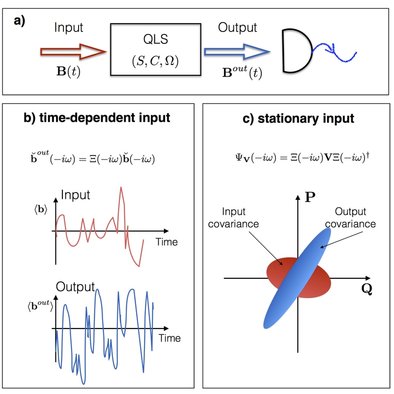
Identification of quantum linear systems: the transfer function approach
The purpose of this project is to investigate system identification for single input single output general (active or passive) quantum linear systems. For a given input we address the following questions: (1) Which parameters can be identified by measuring the output ? (2) How can we construct a system realisation from sufficient input-output data?
We show that for time-dependent inputs, the systems which cannot be distinguished are related by symplectic transformations acting on the space of system modes. Additionally, if the system is known to be passive, then the equivalence classes are characterised by unitary transformations.
We define the notion of global minimality for a given power spectrum, and characterise globally minimal systems as those with fully mixed stationary state.
Relevant publications:
Matthew Levitt, Madalin Guta, Identification of SISO quantum linear systems, Phys. Rev A 95 033825 (2017)
arXiv:1608.01227
M. Guta and N. Yamamoto, System identification for passive quantum linear systems, IEEE Transactions on Control, 61, 921 - 936 (2016)
arXiv:1303.3771v2
The purpose of this project is to investigate system identification for single input single output general (active or passive) quantum linear systems. For a given input we address the following questions: (1) Which parameters can be identified by measuring the output ? (2) How can we construct a system realisation from sufficient input-output data?
We show that for time-dependent inputs, the systems which cannot be distinguished are related by symplectic transformations acting on the space of system modes. Additionally, if the system is known to be passive, then the equivalence classes are characterised by unitary transformations.
We define the notion of global minimality for a given power spectrum, and characterise globally minimal systems as those with fully mixed stationary state.
Relevant publications:
Matthew Levitt, Madalin Guta, Identification of SISO quantum linear systems, Phys. Rev A 95 033825 (2017)
arXiv:1608.01227
M. Guta and N. Yamamoto, System identification for passive quantum linear systems, IEEE Transactions on Control, 61, 921 - 936 (2016)
arXiv:1303.3771v2
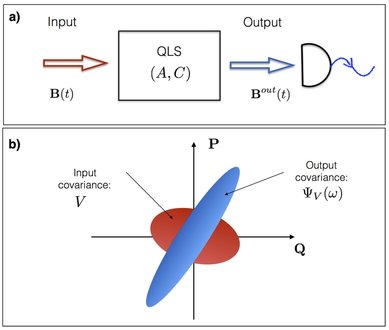
Power Spectrum Identification for Quantum Linear Systems
We investigate system identification for general quantum linear systems. We consider the situation where the input field is prepared as stationary (squeezed) quantum noise. In this regime the output field is characterised by the power spectrum, which encodes covariance of the output state. We address the following two questions: (1) Which parameters can be identified from the power spectrum? (2) How to construct a system realisation from the power spectrum? The power spectrum depends on the system parameters via the transfer function. We show that the transfer function can be uniquely recovered from the power spectrum, so that equivalent systems are related by a symplectic transformation.
Relevant publication:
Matthew Levitt, Madalin Guta, Hendra I. Nurdin, Power Spectrum Identification for Quantum Linear Systems, Automatica 90 255-262 (2018)
arXiv:1612.02681
We investigate system identification for general quantum linear systems. We consider the situation where the input field is prepared as stationary (squeezed) quantum noise. In this regime the output field is characterised by the power spectrum, which encodes covariance of the output state. We address the following two questions: (1) Which parameters can be identified from the power spectrum? (2) How to construct a system realisation from the power spectrum? The power spectrum depends on the system parameters via the transfer function. We show that the transfer function can be uniquely recovered from the power spectrum, so that equivalent systems are related by a symplectic transformation.
Relevant publication:
Matthew Levitt, Madalin Guta, Hendra I. Nurdin, Power Spectrum Identification for Quantum Linear Systems, Automatica 90 255-262 (2018)
arXiv:1612.02681
|
Efficient quantum tomography with incomplete measurement settings
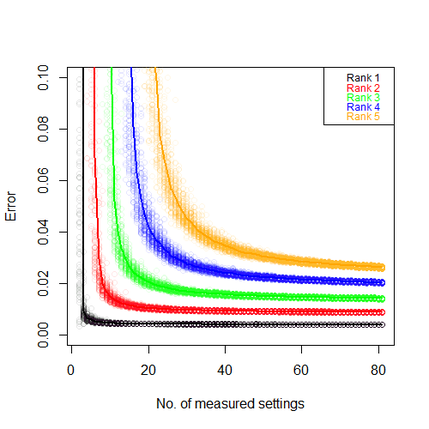
The construction of physically relevant low dimensional state models, and the design of appropriate measurements are key issues in tackling quantum state tomography for large dimensional systems. We consider the statistical problem of estimating low rank states in the set-up of multiple ions tomography, and investigate how the estimation error behaves with a reduction in the number of measurement settings, compared with the standard ion tomography setup. We present extensive simulation results showing that the error is robust with respect to the choice of states of a given rank, the random selection of settings, and that the number of settings can be significantly reduced with only a negligible increase in error. We present an argument to explain these findings based on a concentration inequality for the Fisher information matrix. In the more general setup of random basis measurements we use this argument to show that for certain rank $r$ states it suffices to measure in $O(r\log d)$ bases to achieve the average Fisher information over all bases. Relevant publication: Anirudh Acharya, Theodore Kypraios, M. Guta, Statistically efficient tomography of low rank states with incomplete measurements New Journal of Physics, 18 043018 (2016) |
Fig. Asymptotic mean square error as a function of number of (randomly chosen) measurement settings, for states of different ranks. |

Statistical analysis of low rank tomography with compressive random measurements
We consider the statistical problem of `compressive' estimation of low rank states with random basis measurements, where the estimation error is expressed terms of two metrics - the Frobenius norm and quantum infidelity. It is known that unlike the case of general full state tomography, low rank states can be identified from a reduced number of observables' expectations. Here we investigate whether for a fixed sample size N, the estimation error associated with a `compressive' measurement setup is `close' to that of the setting where a large number of bases are measured. In terms of the Frobenius norm, we demonstrate that for all states the error attains the optimal rate $rd/N$ with only $O(r \log{d})$ random basis measurements.
Relevant publication:
Anirudh Acharya, Madalin Guta, Statistical analysis of compressive low rank tomography with random measurements,
Journal of Physics A: Mathematical and Theoretical, 50 195301 (2017)
arXiv:1609.03758
We consider the statistical problem of `compressive' estimation of low rank states with random basis measurements, where the estimation error is expressed terms of two metrics - the Frobenius norm and quantum infidelity. It is known that unlike the case of general full state tomography, low rank states can be identified from a reduced number of observables' expectations. Here we investigate whether for a fixed sample size N, the estimation error associated with a `compressive' measurement setup is `close' to that of the setting where a large number of bases are measured. In terms of the Frobenius norm, we demonstrate that for all states the error attains the optimal rate $rd/N$ with only $O(r \log{d})$ random basis measurements.
Relevant publication:
Anirudh Acharya, Madalin Guta, Statistical analysis of compressive low rank tomography with random measurements,
Journal of Physics A: Mathematical and Theoretical, 50 195301 (2017)
arXiv:1609.03758
Spectral thresholding quantum tomography for low rank states
The estimation of high dimensional quantum states is an important statistical problem arising in current quantum technology applications. A key example is the tomography of multiple ions states, employed in the validation of state preparation in ion trap experiments. Since full tomography becomes unfeasible even for a small number of ions, there is a need to investigate lower dimensional statistical models which capture prior information about the state, and to devise estimation methods tailored to such models. In this paper we propose several new methods aimed at the efficient estimation of low rank states and analyse their performance for multiple ions tomography. All methods consist in first computing the least squares estimator, followed by its truncation to an appropriately chosen smaller rank. The latter is done by setting eigenvalues below a certain ``noise level" to zero, while keeping the rest unchanged, or normalising them appropriately. A typical MSE rates result is as follows:
The estimation of high dimensional quantum states is an important statistical problem arising in current quantum technology applications. A key example is the tomography of multiple ions states, employed in the validation of state preparation in ion trap experiments. Since full tomography becomes unfeasible even for a small number of ions, there is a need to investigate lower dimensional statistical models which capture prior information about the state, and to devise estimation methods tailored to such models. In this paper we propose several new methods aimed at the efficient estimation of low rank states and analyse their performance for multiple ions tomography. All methods consist in first computing the least squares estimator, followed by its truncation to an appropriately chosen smaller rank. The latter is done by setting eigenvalues below a certain ``noise level" to zero, while keeping the rest unchanged, or normalising them appropriately. A typical MSE rates result is as follows:

Relevant publication:
Cristina Butucea, M. Guta, Theodore Kypraios, Spectral thresholding quantum tomography for low rank states,
New Journal of Physics, 17 113050 (2015)
|
Equivalence classes and local asymptotic normality in system identification for quantum Markov chains
We consider the problems of identifying and estimating dynamical parameters of (ergodic) quantum Markov chains (discrete time), when only the stationary output is accessible for measurements. We show that the knowledge of the output state completely fixes the dynamics up to a `coordinate transformation' consisting of a multiplication by a phase and a unitary conjugation of the Kraus operators. When the dynamics depends on an unknown parameter, we show that the latter can be estimated at the `standard' rate n^{-1/2}, and give an explicit expression of the (asymptotic) quantum Fisher information of the output, which is proportional to the Markov variance of a certain `generator'. More generally, we show that the output is locally asymptotically normal, i.e. it can be approximated by a simple quantum Gaussian model consisting of a coherent state whose mean is related to the unknown parameter.
Relevant publications: M. Guta, J. Kiukas, Equivalence classes and local asymptotic normality in system identification for quantum Markov chains, Commun. Math. Phys. 335 1397-1428 (2015) |
Information geometry and local asymptotic normality for multi-parameter estimation of quantum Markov dynamics
This paper deals with the problem of identifying and estimating dynamical parameters of continuous-time quantum open systems, in the input-output formalism. 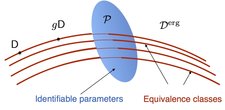
First, we characterise the space of identifiable parameters for ergodic dynamics, assuming full access to the output state for arbitrarily long times, and show that the equivalence classes of undistinguishable parameters are orbits of a Lie group acting on the space of dynamical parameters. Second, we define an information geometric structure on this space, including a principal bundle given by the action of the group, as well as a compatible connection, and a Riemannian metric based on the quantum Fisher information of the output. We compute the metric explicitly in terms of the Markov covariance of certain "fluctuation operators", and relate it to the horizontal bundle of the connection. Third, we show that the system-output and reduced output state satisfy local asymptotic normality, i.e. they can be approximated by a Gaussian model consisting of coherent states of a multimode continuos variables system constructed from the Markov covariance ``data". Relevant publications: M. Guta, J. Kiukas, Information geometry and local asymptotic normality for multi-parameter estimation of quantum Markov dynamics, arxiv:1601.04355 |
Quantum Local Asymptotic Normality
|
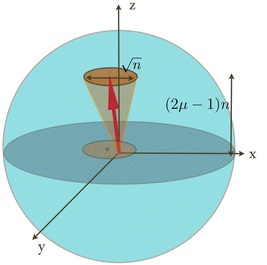
Fig 1. The "big Bloch sphere" of n iid spins. The collective spin vector is has quantum Gaussian fluctuations in the x-y plane and (independent) classical Gaussian fluctuations in the direction z.
Fig 2. Using QLAN, the optimal state estimation problem is asymptotically equivalent (locally in the parameter space) to the simpler problem of estimating the unknown displacement of a hybrid classical-quantum Gaussian state with known covariance and commutation relations. The optimal measurement for the latter is typically of a heterodyne type.
|
|
Local Asymptotic Normality and Fisher Information for the atom maser
System identification is closely related to control theory and plays an increasing role in quantum engineering. In the quantum set-up, system identification is usually equated to process tomography, i.e. estimating a channel by probing it repeatedly with different input states. However for quantum dynamical systems like quantum Markov processes, it is more natural to consider the estimation based on continuous measurements of the output, with a given input which may be stationary. We address this problem using asymptotic statistics tools, in a general setting and for the specific example of estimating the Rabi frequency of an atom maser. We compute the Fisher information of different measurement processes as well as the quantum Fisher information for general Markov processes, in particular the atom maser (see Figs 1&2) and establish the local asymptotic normality of these statistical models. The quantum state of the output carries information about the parameter, and we compute its quantum Fisher information (see Fig 3). The different Fisher informations can be expressed in terms of spectral properties of certain deformed Markov generators and the connection to large deviations is explored. Relevant publications: C. Catana, M. van Horssen and M. Guta Asymptotic inference in system identification for the atom maser Philosophical Transactions of the Royal Society A 370, 5308-5323 (2012) Arxiv:1112.2080 C. Catana, M. Guta and T. Kypraios Maximum likelihood versus likelihood-free quantum system identification in the atom maser, J. Phys. A: Math. Theor. 47 415302 (2014) Fig 3. Quantum Fisher information (black) for the atom maser output (i.e. outgoing atoms and em bath). For comparison, classical Fisher informations for two thought experiments: following the cavity jumps (red) and with additional information concerning the nature of the UP jump (exchange of photon with an atom, or absorption from the bath) (blue).
|
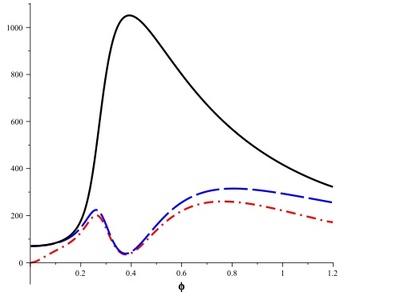
Fig 1. Classical Fisher information (asymptotic per time unit) for 3 different atom maser counting statistics, as function of the Rabi frequency phi: number of excited atoms (black), ground state atoms (blue), and both types (red). Note the strong dependence on phi, with zero Fisher information at the point where the the mean photon number of the cavity's stationary state is maximum.
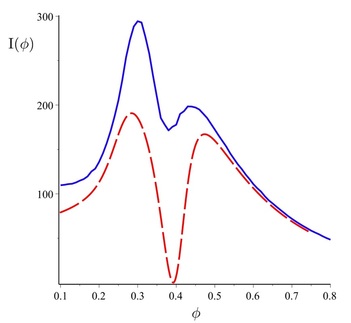
Fig 2. Classical Fisher information for total counts (red) versus full counting statistics (blue) as function of the Rabi frequency phi. The latter is obtained by performing maximum likelihood estimation, and is significantly larger than the former around phi = 0.4 where the mean photon number of the cavity's stationary state is maximum.
|
|
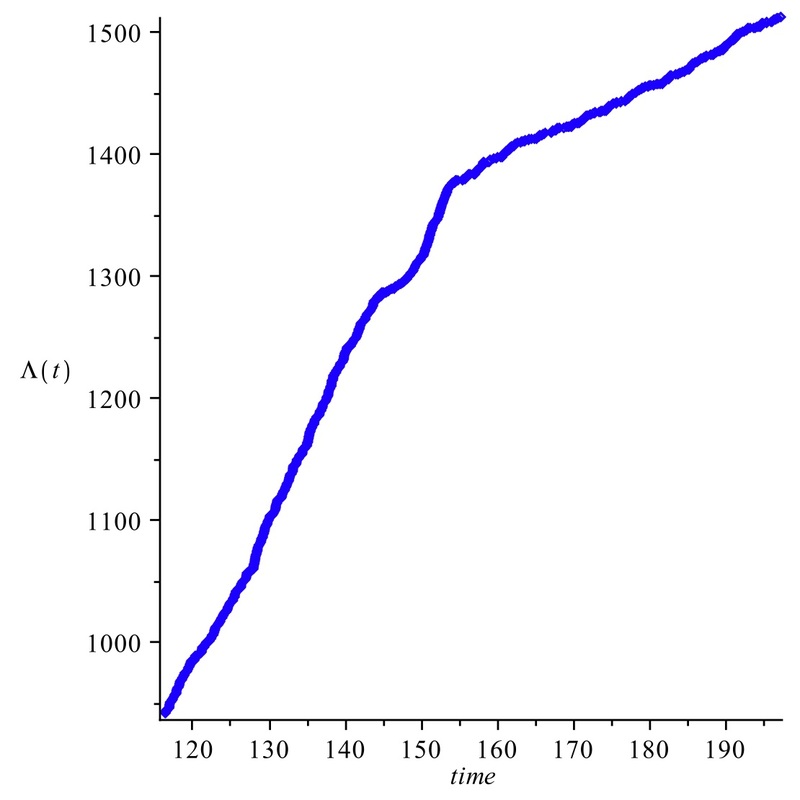
Large Deviations and Dynamical Phase Transitions
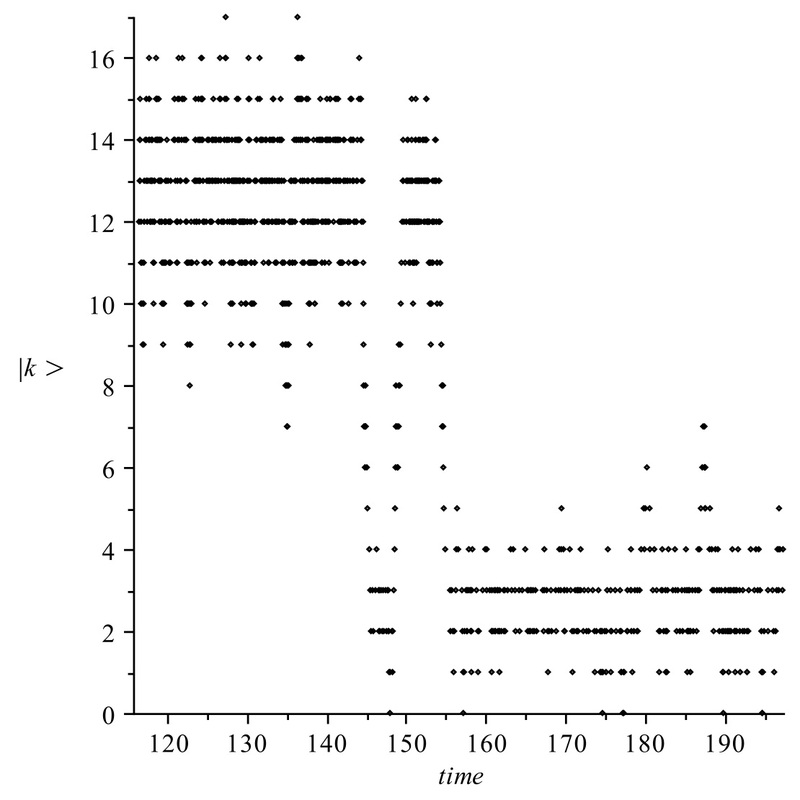
for Open Quantum Systems Open systems can be monitored indirectly via continuous-time measurements on the environment. The measurement trajectories determine the conditional evolution of the system through stochastic master (or filtering) equations. Dynamical phase transitions of the open system are characterised by the existence of different phases in the space of trajectories seen as "configurations" of a stochastic system (see Fig. 1 for the case of the atom maser). Mathematically, the long time behaviour is determined by the Large Deviations Theory, which describes the exponential decay of probability for trajectories "deviating from the mean". The corresponding rate function is equal to the first derivative of the dominant eigenvalue of a Lindblad-type generator (see Fig 2). Phase transitions are characterised by jumps in the rate function and the near-degeneracy of the dominant eigenvalue (see Fig. 3) Relevant publications: I. Lesanovsky, M. van Horssen, M. Guta, J. P. Garrahan Characterization of dynamical phase transitions in quantum jump trajectories beyond the properties of the stationary state Phys. Rev. Lett. 110, 150401(2013) Arxiv:1211.1918 M. van Horssen and M. Guta Large deviations and dynamical phase transitions for the atom maser Arxiv: 1206.4956 Fig 1. Left panel: jump evolution of the atom maser exhibiting a phase transition between a high and a low photon number phase. Right panel: the phase transition is captured by the process counting the total number of ground state atoms detected up to time t.
|
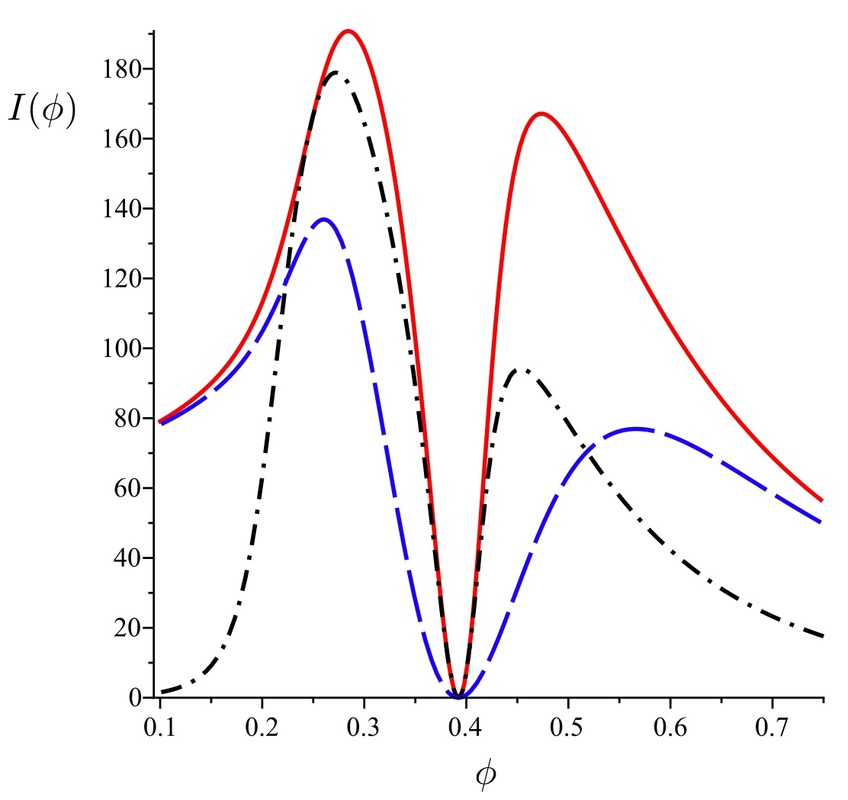
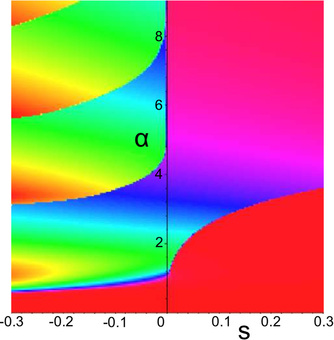
Fig 2. Large deviations rate function for total ground state atoms counts, as function of the "counting field" s and the Rabi parameter alpha. Phase transitions correspond to jumps in the rate function.
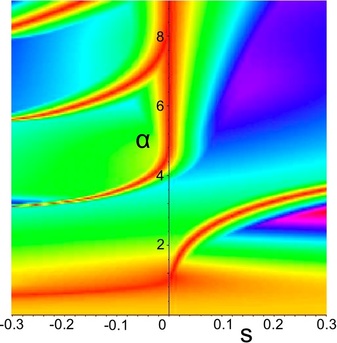
Fig 3. Spectral gap of the Lindblad generator as function of the "counting field" s and the Rabi parameter alpha. Gap closes in the region where the rate function has a jump.
|
Model selection in Quantum Tomography
Statistical inference has become a key component of many quantum engineering experiments where quantum states and processes need to be estimated from the measurement data. However, the reconstruction of the quantum state (quantum tomography) becomes unfeasible even for systems made up of a small number of components, due to the exponential scaling of the state space dimension. Therefore, one needs to exploit prior information and the sparsity properties of the experimental state in order to reduce the dimensionality of the estimation problem.
We propose model selection as a general principle for finding the simplest, or most parsimonious explanation of the data, by fitting different models and choosing the estimator with the best trade-off between likelihood fit and model complexity. We apply two well established model selection methods: the Akaike information criterion (AIC) and the Bayesian information criterion (BIC), and assess their performance first on simulated data; namely on randomly chosen low rank states of 1 and 4 ions. We also apply the methodology to real data from a 4 ions experiment performed by Rainer Blatt’s group. Relevant publication: M. Guta, T. Kypraios and I. Dryden Rank based model selection for multiple ions quantum tomography New Journal of Physics, 14, 105002 (2012) Arxiv: 1206.4032 |
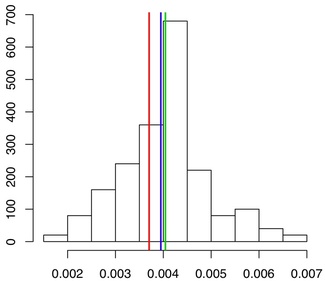
Histogram of the norm-two error of the maximum likelihood estimator (MLE) for 100 samples from a pure state. The mean square error (green line) of the MLE is very close to the classical Cramer-Rao bound (blue line) as predicted by asymptotic theory, and the latter is only slightly larger than the “quantum optimal bound” (red line), showing that for pure states the ions measurement is almost almost optimal among all measurements!
|
Quantum Metrology
Quantum precision enhancement is of fundamental importance for the development of advanced metrological optical experiments, such as gravitational wave detection and frequency calibration with atomic clocks. Precision in these experiments is strongly limited by the 1/N shot noise factor with N being the number of probes (photons, atoms) employed in the experiment.
Quantum theory provides tools to overcome the bound by using entangled probes (see figure on the right side). In an idealized scenario this gives rise to the Heisenberg scaling of precision 1/N. Here we show that when decoherence is taken into account, the maximal possible quantum enhancement in the asymptotic limit of infinite N amounts generically to a constant factor times 1/sqrt(N) rather than the quadratic improvement 1/N. We provide efficient and intuitive tools for deriving the bounds based on the geometry of quantum channels and semi-definite programming. We apply these tools to derive bounds for models of decoherence relevant for metrological applications including: depolarization, dephasing, spontaneous emission and photon loss (see table on the right side). Relevant publication: R. Demkowicz-Dobrzanski, J. Kolodynski and M. Guta, The elusive Heisenberg limit in quantum-enhanced metrology, Nature Communications, 3, 1063 (2012) Arxiv: 1201.3940 |
Quantum Homodyne Tomography as an ill posed statistical inverse problem
I collaborated with Luis Artiles, Richard Gill, Cristina Butucea on devising non-parametric estimation methods for Quantum Homodyne Tomography (QHT). The probability distribution of the data is obtained by taking the Radon transform of the Wigner function followed by performing a Bernoulli convolution accounting for the detection inefficiency. The inverse map is unbounded, so we deal with an ill posed inverse problem, which requires some form of regularisation e.g cut-off in frequency or dimension of the density matrix. Some of our results are illustrated below.
Relevant publications: C. Butucea, M. Guta and L. Artiles Minimax and adaptive estimation of the Wigner function in quantum homodyne tomography with noisy data Annals of Statistics, 35, 465-494 (2007) math.ST/0504058 M. Guta and L. Artiles Minimax estimation of the Wigner function in Quantum Homodyne Tomography with ideal detectors Mathematical Methods of Statistics, 16, (2007), 1-15 math.ST/0611117 L.Artiles, M. Guta and R.D. Gill An invitation to quantum tomography Journal of the Royal Statistical Society B: Methodology 67, (2005), 109-134 math.ST/0405595 |
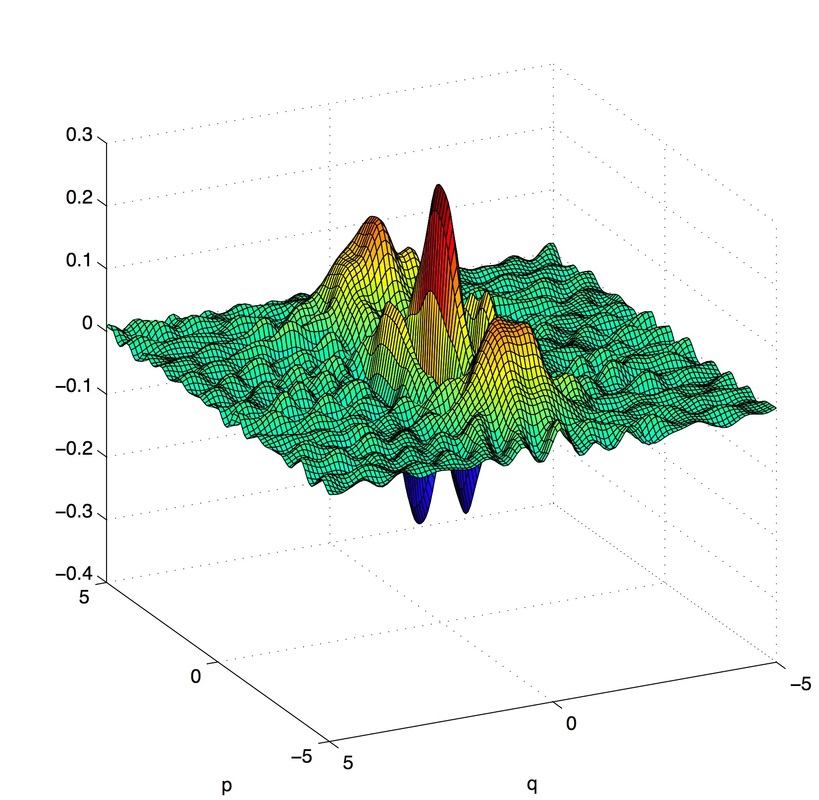
Noise deconvolution in Wigner function estimation
Estimated Wigner function of a Schrodinger cat state in Quantum Homodyne Tomography with detection efficiency 90%. The estimator is based on 100000 data and performs both inverse Radon Transform and noise deconvolution.
|
Model selection by
|
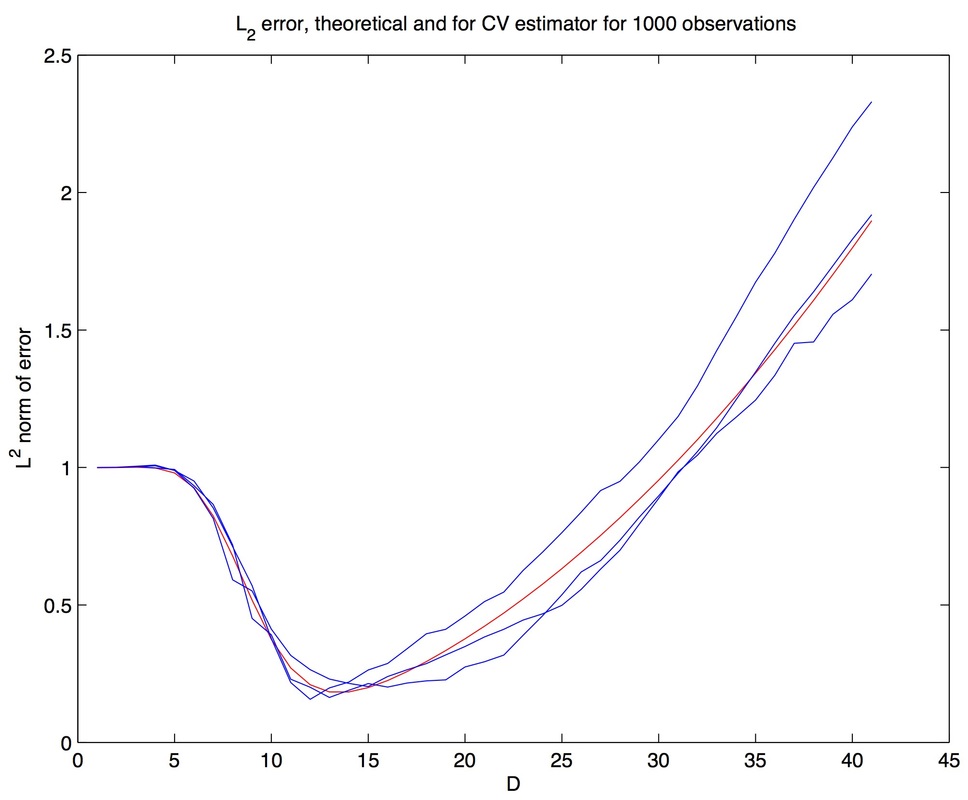
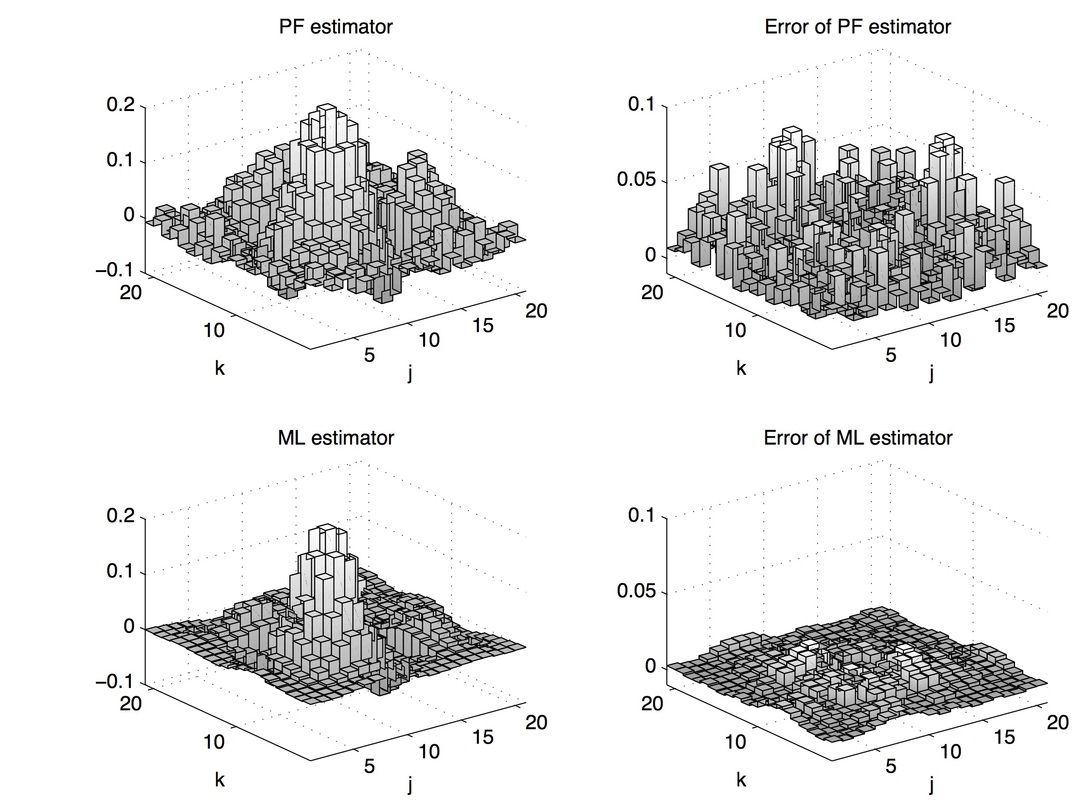
Pattern functions vs MLE
The density matrix of a squeezed state is estimated using pattern functions and maximum likelihood estimators, the former appearing to be more noisy than the latter (see right panels with errors). The dimensions of each matrix estimator is chosen to be optimal for that type of estimator. The maximum likelihood estimator is however much more expensive in terms of computational time.
|