 Immunotherapy simulation (jpeg).
Immunotherapy simulation (jpeg). Juxtacrine intercellular signalling
The effect of predation on biological invasions
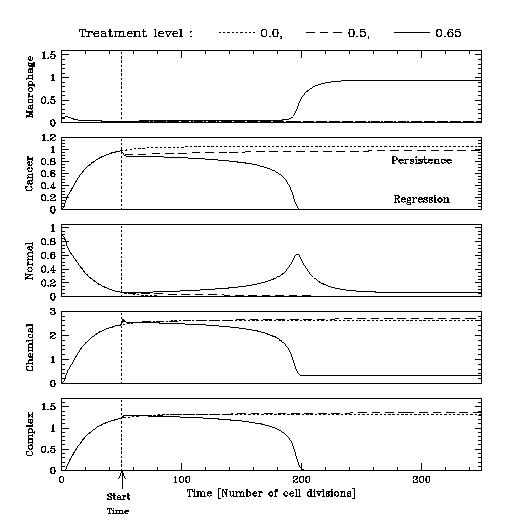
Even in the early stages of their development, tumours are not simply a homogeneous grouping of mutant cells; rather, they develop in tandem with normal tissue cells, and also recruit other cell types. Many solid tumours contain a high proportion of macrophages, a type of white blood cell which can have a variety of effects upon the tumour, leading to a delicate balance between growth promotion and inhibition.
 Immunotherapy simulation (jpeg).
Immunotherapy simulation (jpeg).
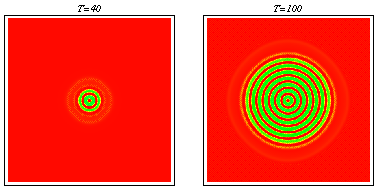
2d simulation showing evolution of a pattern behind a travelling wave of tumour invasion.
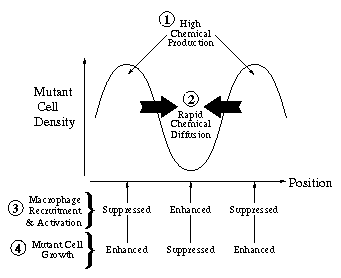 An intuitive explanation for this spatial instability is that given a local perturbation increasing the density of mutant cells, chemical regulator production will also increase locally. Then if the chemical diffuses fast enough, it will act non-locally to activate macrophages to the tumouricidal state and to stimulate an additional influx of macrophages. This will suppress non-local mutant cell growth, whilst enhancing local mutant cell growth, due to the relative suppression of local macrophage activation, so that the original perturbation will grow in time.
An intuitive explanation for this spatial instability is that given a local perturbation increasing the density of mutant cells, chemical regulator production will also increase locally. Then if the chemical diffuses fast enough, it will act non-locally to activate macrophages to the tumouricidal state and to stimulate an additional influx of macrophages. This will suppress non-local mutant cell growth, whilst enhancing local mutant cell growth, due to the relative suppression of local macrophage activation, so that the original perturbation will grow in time.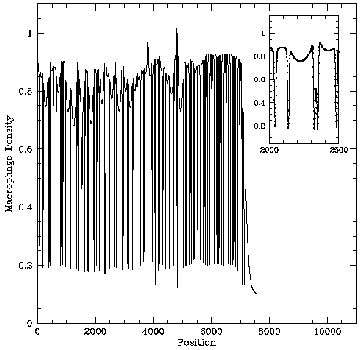 PDE model -- spatiotemporal irregularity: Using data from the literature I determined ranges for the parameters governing macrophage motility using a mathematical model of the experimental procedure. Including macrophage chemotaxis with these parameters led to the development of irregular wakes behind the wave front of invading tumour cells. This phenomenon was investigated using domain length as a bifurcation parameter. Stable oscillating solutions with a regular period were found to coexist with stable steady patterns for certain windows in domain length which were deduced to appear at regular intervals. Intuitively the wave front can be treated as a moving boundary, leading to the proposal that as the wave spreads out, the effective domain length passes through a series of bifurcations, so that the solution seen is always transient and irregular.
PDE model -- spatiotemporal irregularity: Using data from the literature I determined ranges for the parameters governing macrophage motility using a mathematical model of the experimental procedure. Including macrophage chemotaxis with these parameters led to the development of irregular wakes behind the wave front of invading tumour cells. This phenomenon was investigated using domain length as a bifurcation parameter. Stable oscillating solutions with a regular period were found to coexist with stable steady patterns for certain windows in domain length which were deduced to appear at regular intervals. Intuitively the wave front can be treated as a moving boundary, leading to the proposal that as the wave spreads out, the effective domain length passes through a series of bifurcations, so that the solution seen is always transient and irregular.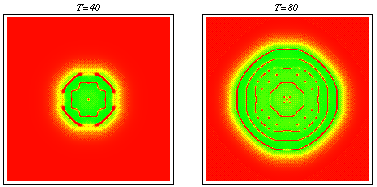 Snapshots from a two-dimensional simulation illustrating that chemotaxis leads to solutions which are irregular in space and time. For a movie of a similar simulation, click here: Chemotaxis induces spatiotemporal irregularities (mpeg) and another example (mpeg).
Snapshots from a two-dimensional simulation illustrating that chemotaxis leads to solutions which are irregular in space and time. For a movie of a similar simulation, click here: Chemotaxis induces spatiotemporal irregularities (mpeg) and another example (mpeg).
Experimental studies have revealed the propagation of travelling bursts of activity in cortical and thalamic brain slices. Experiments in primates have also revealed that prefrontal cortical networks can support spatially localized areas of high activity, thought to be important for the functioning of working memory. Such waves and bumps of firing rate activity are a consequence of non-local synaptic interactions and the intrinsic behavior of local neuronal circuitry. The mathematical description of synaptically coupled neural tissue typically involves the use of integral equations. Apart from a spatial integral mixing the network connectivity function with space-dependent delays, arising from non-instantaneous axonal communication, these integral models can also include a temporal integration over some appropriately identified distributed delay kernel. These distributed delay kernels are biologically motivated and represent the response of biological synapses to spiking inputs. I am interested in using techniques from dynamical systems theory to study waves and patterns in such integral neural field models. This work is being done in collaboration with Steve Coombes, Gabriel Lord and Tony Humphries.
Relevant publications:
S Coombes G J Lord and M R Owen 2003 Waves and bumps in neuronal networks with axo-dendritic synaptic interactions, Physica D, Vol 178, 219-241
S Coombes and M R Owen 2004 Evans functions for integral neural field equations with Heaviside firing rate function SIAM Journal on Applied Dynamical Systems (to appear)
Juxtacrine signalling is emerging as an important means of cellular communication, in which signalling molecules anchored in the cell membrane bind to and activate receptors on the surface of immediately neighbouring cells. We have developed a mathematical model to describe this process, consisting of a coupled system of ordinary differential equations, with one identical set of equations for each cell. We use a generic representation of ligand--receptor binding, and assume that binding exerts a positive feedback on the secretion of new receptors and ligand. We have also developed continuous analogues of this discrete model, and demonstrated that they have much the same properties.
 Evolution of spots and stripes via juxtacrine signalling.
The figure shows the evolution of patterns from a small initial
perturbation of a uniform equilibrium, in a 60x30 grid of cells.
Two cases are shown, with different parameters, one giving a spotted
pattern and the other giving a striped pattern.
The plots show unoccupied receptor numer (blue=low, red=high), and
there are corresponding patterns in ligand and bound receptors.
Evolution of spots and stripes via juxtacrine signalling.
The figure shows the evolution of patterns from a small initial
perturbation of a uniform equilibrium, in a 60x30 grid of cells.
Two cases are shown, with different parameters, one giving a spotted
pattern and the other giving a striped pattern.
The plots show unoccupied receptor numer (blue=low, red=high), and
there are corresponding patterns in ligand and bound receptors.
Observations on Mount St. Helens indicate that the spread of recolonising lupin plants has been slowed due to the presence of insect herbivores and it is possible that the spread of lupins could be reversed in the future by intense insect herbivory. We are investigating mechanisms by which herbivory can contain the spatial spread of recolonizing plants. Our approach is to analyse a series of predator-prey reaction-diffusion models and spatially coupled ordinary differential equation models to derive conditions under which predation pressure can slow, stall or reverse a spatial invasion of prey. Further developments will include work on integrodifferential equation models, and the effect of prey quality on predation rates.
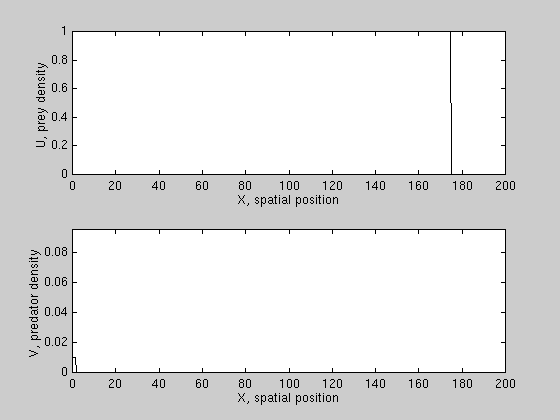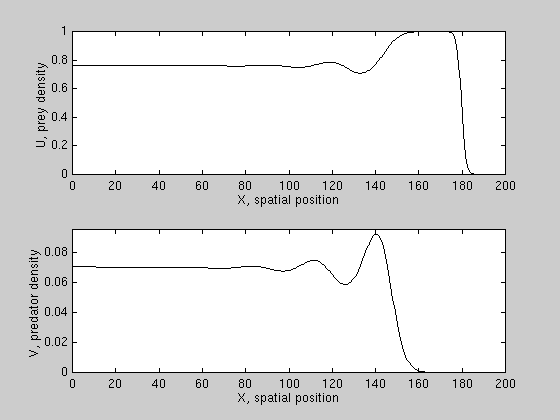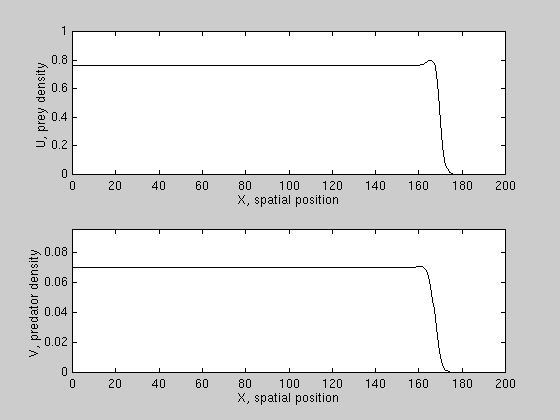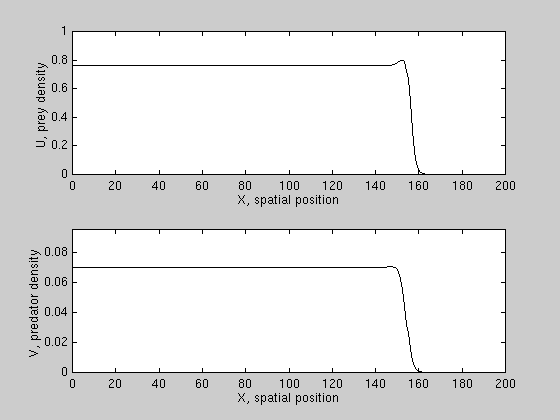 We have derived conditions for wave reversal for a class of PDE models,
and found that predation can reverse prey invasion only if prey growth is
subject to a "strong" allee effect, i.e. prey growth per capita is negative
at low densities. An example is shown here.
We have derived conditions for wave reversal for a class of PDE models,
and found that predation can reverse prey invasion only if prey growth is
subject to a "strong" allee effect, i.e. prey growth per capita is negative
at low densities. An example is shown here.
The minimal integrate-and-fire-or-burst (IFB) neuron model reproduces the salient features of experimentally observed thalamocortical relay neuron response properties, including the temporal tuning of both tonic spiking (i.e, conventional action potentials) and post-inhibitory rebound bursting mediated by the low-threshold Ca2+ current, IT. In collaboration with Greg Smith and Steve Coombes I am developing an exact theory of mode-locking under the influence of arbitrary periodic forcing. In this analysis, the instabilities of mode-locked states are identified as both smooth bifurcations of an associated firing time map and non-smooth bifurcations of the underlying discontinuous flow.
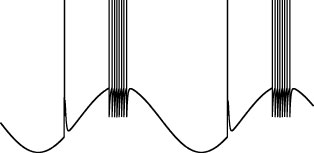
High frequency oscillation (HFO) is a method of mechanical ventilation where small volume, high frequency breaths (>2 Hz.) are administered to the lung, a radical departure from normal respiration or conventional mechanical ventilation where large tidal volume breaths are given at low frequencies (less than 0.25 Hz.).
Damage from air leaks is one of the most frequent life threatening complications resulting from mechanical ventilation. A major goal of HFO is to facilitate gas transfer in diseased or premature lungs without damaging them. Studies have shown that the smaller than usual tidal volumes and the lower pressure variations found in HFO can help to achieve this goal.
Since the breath volumes administered in HFO are much smaller than the
volume necessary to fill the lungs, the question arises as to how HFO
can ventilate at all. Convective dispersion of gas in the bronchi due
to asymmetric flow profiles during inspiration and expiration and
alveolar ventilation by out-of-phase oscillations are thought to be
significant. Such out-of-phase oscillations arise from the
differential filling of parallel lung units that have different time
constants. The result is a ``sloshing" motion of air between the two
neighboring units during a ventilation cycle (pendelluft).
Follow this link to the IBIS home page
Mathematical and Numerical Modeling Approach: Even with modern
parallel computational methods the number of alveolar sacs in a
typical lung (approximately 300 million) and the range of space scales
in lung tissue preclude a numerical simulation of the entire fluid
dynamical and fluid-wall interactions for the whole lung. Our
approach is two-fold: (i) homogenized mathematical model, based on the
microscopic structure of alveolar sacs, to give macroscopic properties
of large groups of alveolar sacs (acini) that comprise the lung
tissue. The homogenization method allows us to ``average'' over the
lung microstructure, yielding macroscopic properties. (ii) a
numerical fluid-dynamic simulation model of large-scale respiratory
flow. Our long-range goal is to link these two approaches with a
series of intermediate numerical models, linking macroscopic
properties of lung tissue to fluid flow.
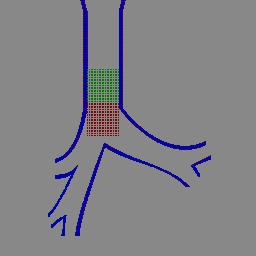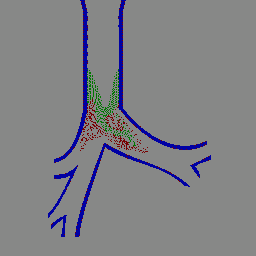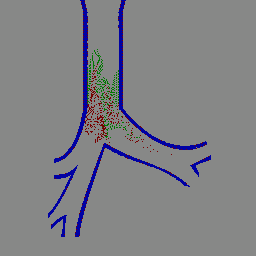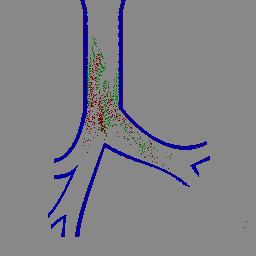 IBIS lung simulation (animated GIF)
IBIS lung simulation (animated GIF)
This section is under construction...still